CLS(Classical Least Square:古典的最小二乗法)
MIDAC社FT-IRガス分析計の定量ソフトウェアAutoQuantは、サンプル中の化合物濃度を予測するために古典的最小二乗法(CLS)アルゴリズム計算を使用しています。
「古典的」という名がついているのはベールの法則における古典的な原理に基づいているからです。
A = K・C [1]
- A:与えられた波数における吸光度
- K:同波数における吸光係数と光路長の積
- C:化合物の濃度
Kは濃度既知のスペクトルから求めることができます。Kがわかれば、化合物スペクトルの吸光度から濃度を求めることができます。
C = A/ K [2]
CLSはある与えられた波数における単一の成分に対する[2]の式を重回帰分析に適用したものです。これを複数の成分および波数に適用すると次の式になります
Aw = ∑c=1,n Kwc・Cc [3]
- Aw: w番目の波数における吸光度
- Kwc: w番目の波数におけるc番目の成分に対する吸光係数
- Cc: C番目の成分の濃度
- 全成分の数
これを拡張すると…
- A1 = K11・C1+K12・C2+……+K1c・Cc
- A1 = K21・C1+K22・C2+……+K2c・Cc
- A1 = K31・C1+K32・C2+……+K3c・Cc
・
・
・
- A1 = Kw1・C1+Kw2・C2+……+Kwc・Cc [4]
[4]は行列を用いてA = KC [5]とも表現できます。
CLSメソッドを校正するには濃度既知の単一成分で構成された校正用セットを作成します。
次に式[5]よりKを求めます。
AとCを求める際に不確かさが存在するため式[5]を解くには最小二乗法が最適であり、誤差の二乗和を最小にするKが解になります。
誤差 = KC-AC [6]
上の式に対するくわしい解法についてはここでは触れませんので線形代数の教科書をご参照いただくこととして、最終的には下記濃度未知の成分に対する校正用行列Kcalが求まります
| Cunk=Kcal・Aunk |
つまり、CLSはサンプルスペクトルを一群の参照スペクトルと比較する手法と言えます。
最小二乗法では、サンプルスペクトルを再現する際に加算していく参照スペクトルの比率を計算します。この比率がサンプル中の各成分の濃度になります。
ここでCLSは吸光度と濃度の間に比例関係があることを前提にしていることにご注意ください。
実際に測定する際はスペクトルの全てのデータポイントを使うことはありません。
与えられた化合物でピークが生じる波数域だけを使います。これを分析波数域といいます。
校正において他の成分が同じ波数域で吸収ピークを持つ場合もあるので、CLSアルゴリズムが干渉成分も考慮するよう干渉成分も登録しなければなりません。
成分毎に選択する分析波数域も異なるため、各成分に対して別々にCLSを行います。 AutoQuantはこの処理を自動化してユーザーが一回測定するだけで済むようにしています。
非線形およびサブメソッド
ベールの法則は一次式で表わされます。この法則は吸光度が濃度に比例し、ピークが干渉する波気体のサンプルではこの傾向が特に顕著です。こうした化合物を「直線性が低い」化合物と呼びます。
このようなケースではサンプルの濃度が参照スペクトルの濃度に近くいなければ、正しい結果が得られません。これに対処するためには予想される濃度レンジをカバーするなるべく多くの参照スペクトルを使用します。濃度の近い隣接参照スペクトル間では挙動はより線形に近くなります。つまり、直線性の低い化合物でも濃度レンジを狭くすれば直線性の高い化合物と同じ扱いができるということです。このサンプル濃度を2つの参照スペクトルで細分化し2つのCLS演算の結果から内挿することを「区分線形内挿法」と呼びます。
AutoQuantは参照スペクトルデータポイント間を結ぶ改良キュービックスプライン補間演算処理法を採用しているため、内挿は単なる線形ではありません。
AutoQuantでは、一つの化合物に複数のスペクトルが含まれている場合、その化合物は非線形であると定義されます。一つのサブメソッドで一つの線形CLS分析を行います。次のメソッドを見て下さい
| 化合物 | 参照スペクトル | 分析波数域 |
| A | A1 | R1 |
| A2 | R1 | |
| A3 | R1 | |
| B | B1 | R2 |
| A2 | R2 | |
| C | C1 | R3 |
| C2 | R3 | |
| C3 | R3 | |
| C4 | R3 |
化合物Aについてのみでも、以下のサブメソッドが考えられます
■(スペクトル、分析波数域)の組み合わせ
| (A1、R1) | (C1、R1) | (B1、R1) | (A2、R1) | (C1、R1) | (B1、R1) | (A3、R1) | (C1、R1) | (B1、R1) | ||
| (A1、R1) | (C2、R1) | (B1、R1) | (A2、R1) | (C2、R1) | (B1、R1) | (A3、R1) | (C2、R1) | (B1、R1) | ||
| (A1、R1) | (C3、R1) | (B1、R1) | (A2、R1) | (C3、R1) | (B1、R1) | (A3、R1) | (C3、R1) | (B1、R1) | ||
| (A1、R1) | (C4、R1) | (B1、R1) | (A2、R1) | (C4、R1) | (B1、R1) | (A3、R1) | (C4、R1) | (B1、R1) | ||
| (A1、R1) | (C1、R1) | (B2、R1) | (A2、R1) | (C1、R1) | (B2、R1) | (A3、R1) | (C1、R1) | (B2、R1) | ||
| (A1、R1) | (C2、R1) | (B2、R1) | (A2、R1) | (C2、R1) | (B2、R1) | (A3、R1) | (C2、R1) | (B2、R1) | ||
| (A1、R1) | (C3、R1) | (B2、R1) | (A2、R1) | (C3、R1) | (B2、R1) | (A3、R1) | (C3、R1) | (B2、R1) | ||
| (A1、R1) | (C4、R1) | (B2、R1) | (A2、R1) | (C4、R1) | (B2、R1) | (A3、R1) | (C4、R1) | (B2、R1) |
化合物BおよびCについても同様の組み合わせを行う
サブメソッドの数がいわゆる「組み合わせの爆発」によって急激に増加することが分かります。このメソッドでも、3×3×2×4=72通りのサブメソッドがあります。しかしAutoQuantによるプロセスの自動化のおかげでユーザーは一回の測定でCLSによる濃度予測および内挿の多くの演算結果が得られます。
区分線形内挿法
AutoQuantは多くのCLSサブメソッドを使用して、最良の結果を与えるサブメソッドを選択し内挿した結果を最終結果とする分析方法です。非線形の化合物を一つにつき濃度が100から400までのスペクトルを4個選択した例を考えてみましょう
| 100 | 0.30 |
| 200 | 0.50 |
| 300 | 0.60 |
| 400 | 0.65 |
ここで各スペクトルを用いて吸光度が0.5の場合の濃度を予想してみましょう。
これはAutoQuantにおいては4個のサブメソッドがあることを意味します。
| サブメソッド | 濃度 | ピーク値0.55の時の予想濃度 |
| 1 | 100 | 183.33 |
| 2 | 200 | 220.00 |
| 3 | 300 | 275.00 |
| 4 | 400 | 338.46 |
2番目のサブメソッドでは2番目および3番目のサブメソッドの参照スペクトル濃度の間の値を予測しています。3番目のサブメソッドも2番目および3番目のサブメソッドの参照スペクトル濃度の間の値を予測しています。これらのメソッドはそれぞれの中間の値を予測しています。しかし1番目および2番目のサブメソッドについては同じことは言えず、予想濃度が参照スペクトル濃度よりも高くなっていることに注目して下さい。同様に3番目および4番目のサブメソッドでは予測値がいずれも参照スペクトルの濃度よりも低くなっています。それでは一体どれが正しいのでしょうか?ここで内挿せずに一つの測定結果だけを選択するとしたら参照スペクトル濃度に一番近い数値である220を選択すべきです。しかし次の加重平均を行い内挿することでより正確な結果が得られるのです
220 * (1 - 20/(300-200)) + 275 * (20/(300-200)) = 220 *.8 + 275 *.2 = 231
上の方法は2番目の予測値から見た加重平均を行っています。AutoQuantは参照スペクトル濃度と予測濃度との近さに応じて、左右のスペクトルから加重平均処理するか両方からの距離がほぼ同じ場合は推移的加重平均処理します。理想的には上のケースでもっと多くのスペクトルを使うべきでした。2つのスペクトルからの予測濃度が大きく異なるという事実は、より精度あるサブメソッドが必要であることが示唆されています。しかしながら、231という結果は単一スペクトルから計算結果を出さなければならない場合よりも正確な予測値です。実際には、濃度予測は上の解説よりも複雑です。
不確かさの計算
AutoQuant4に表示される不確かさの値はCLSによる予測モデルがどれ程フィットしているかの指標となります。不確かさの値は残差スペクトルから計算されます。残差の平均値は0となります。モデルがデータに正確に適合していれば、残差はどこをとっても0になります。AutoQuant4の不確かさの計算方法はHaaland氏の論文における方法と同じです。
AutoQuant4で計算される不確かさの値はHalaand氏の命名により予測濃度の標準誤差、すなわちSECと呼ばれます。周辺標準偏差としても知られています。濃度の不確かさは残差の二乗和の平方根に比例します。前述の式6により残差スペクトルRが得られます。1個のスペクトルに対し分散σ2は次のように計算されます
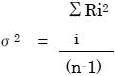
n:データポイントの数
SECは次のように求められます:
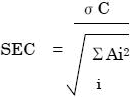
Aはスペクトル強度(吸光度)、Cは参照スペクトルの既知濃度
SECを1.96倍したものが、95%の信頼区間になります。非線形の内挿法を使用するサンプルの場合、不確かさは左と右との隣接スペクトルからの加重平均値が表示されます。
ベースライン補正
参照スペクトルとサンプルスペクトルのベースラインを補正するとCLSの精度が向上することがわかっています。AutoQuantは、0次、1次、2次式でベースラインを補正します。AutoQuantでは0次の処理をオフセット、1次式処理をスロープ、2次式処理をウィグルと称しています。時に一次補正ベースラインあるいは二次補正ベースラインにフィッティングすることができます。さらにAutoQuantでは、全波数域(単一ベースライン)あるいは個々の分析波数域(複数ベースライン)に対してベースライン補正をかけることができます。
温度および圧力補正
理想気体の法則により、容器内の気体の濃度は温度と圧力の影響を受けます。従って気体サンプルを採取する場合は参照気体とサンプルの気体が採取された温度圧力の差異を補正しなければなりません。気体サンプルについては、圧力一定で温度が上昇した場合には吸光度は減少します。温度一定で圧力が増加した場合には吸光度は増加します。
AutoQuant 3では、以下の式を利用して予測した後に補正を行います
- Ct: 温度補正後濃度
- Cp: 圧力補正後濃度
- Co: 予測濃度
- TrおよびTs: 参照気体およびサンプル気体の温度
- PrおよびPs: 参照気体およびサンプル気体の圧力
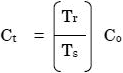
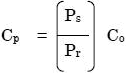
■参考文献
- D.M. HaalandおよびR.G.Easterling; "Improved Sensitivity of Infrared Spectroscopy by the Application of Least Squares Methods" Applied Spectroscopy 34(5):539-548(1980)
- W.C. Hamilton; "Statistics in PhysicalScience Chapter 4" (Ronald PressCo., New York, 1964)
- Rechard Kramer; "Chemometric Techniquesfor Quantative Analysis Chapter 3" (Marcel Dekker Inc., New York, 1998)
- G. Plummer; "Description of a Classical Least SquaresAnalysis Techneique and a Comparison of Two Correction Schemes forNon-Linearity in Measured Sample and Reference Absorbance" Midac Corporation (2001)
- AutoQuant3 On-line Help File, MidacCorporation, (1998)
|
FTIR分析装置のメンテナンスをできる人材を募集しています! お問い合わせはフォームからお願いします。 |
(1)FTIRとは?
(6)他成分の干渉
(7)FTIRの測定可能波数域
(8)FTIR測定の定量方法




